Projects
These research projects are advised or led by Dr. Brittany Terese Fasy, Dr. David L. Millman, and Dr. Binhai Zhu. The focus of the research conducted by CompTaG is applied topological data analysis and computational geometry. Our goal is to apply theoretical knowledge on the subjects to real data sets in new and meaningful ways.
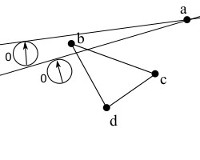
Shape Reconstruction
In this project we are extending work on reconstructing shapes using persistence diagrams. We are currently working on extending our results from our paper "Learning Simplicial Complexes from Persistence Diagrams" that was published at CCCG18.
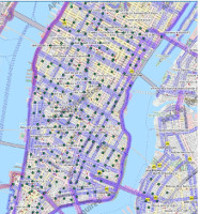
Analyzing Data on Road Networks
In this project we use topological features of data collected on roads and maps to learn about how people move in different infrastructures. We also use this information to see if the current infrastructure is well designed or otherwise. This work is often done in collaboration with Dr. Carola Wenk at Tulane University.
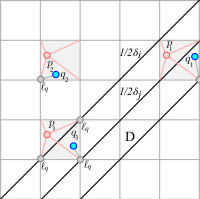
Searching in the Space of Persistence Diagrams
Persistence diagrams are important tools in the field of topological data analysis that describe the presence and magnitude of features in a filtered topological space. In this research project, we apply concepts from locality-sensitive hashing to support approximate nearest neighbor search in the space of persistence diagrams.
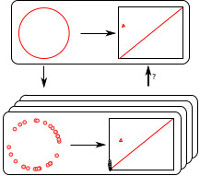
Statistics and Topology
The tools of topological data analysis (TDA), such as persistence diagrams, provide new descriptors of data sets, with the potential to uncover new insights into data. In our research at the intersection of topology and statistics, we define new topological descriptors, and prove statistical properties of these descriptors.
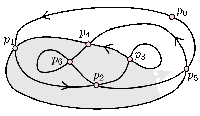
Minimum Homotopy
Finding the minimum area swept out by continuously deforming a closed curve in the plane to a point is an area of active research. One application is measuring the similarity between two sets of GPS coordinates. We use properties of the curves to develop efficient algorithms to find the minimum homotopy area.
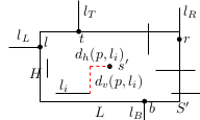
Constrained Facility Location
Facility location is a traditional geometric optimization problem, the objective being optimizing certain geometric criteria to build optimal (or sub-optimal) locations for the facilities. In many modern applications, significant constraints could be placed on the facilities (e.g., a noisy facility should be far away from the residential areas).

Gleason QuBBD Project
The long-term goal of this project is to develop quantitative methodology for detecting geometric and topological features in point clouds extracted from histology images. Of particular relevance, this project considers the setting of prostate cancer classification, which is based on a pathologist grading of histology slides using the Gleason grading system.
BRaiD
Biofilms Resources and Information Database (BRaID) is a centralized database and analysis tool for the diverse types of biofilm-related data such as metagenomics, images, and trajectories. BRaID will give biofilm researchers easier access to large amounts of data and analytical tools.

R Package TDA
The TDA package in R is an important tool for the implementation of key functions used in topological data analysis. We are working to simplify use of the package and enhance its viability in the future by improving and expanding upon its documentation.